Die Notwendigkeit komplexer Zahlen

Auf komplexe Zahlen waren Mathematiker im 18. Jahrhundert gestoßen, als sie immer neue mathematische Aufgaben (Gleichungen) lösen wollten. Die Menge der bekannten Zahlen reichte dazu oft nicht aus und musste erweitert werden, bis sie schließlich auch die komplexen Zahlen beinhaltete.

Zu Anfang kannten Mathematiker ganze Zahlen wie -2, 0, 1, oder 2. Mit ihnen ließen sich Aufgaben wie "Welche ganze Zahl x ergibt mit 2 multipliziert 8?" lösen. Die Antwort lautet x = 4.

Bei der Frage "Welche Zahl x ergibt mit 2 multipliziert 9?" müssen die ganzen Zahlen jedoch passen. Es gibt keine ganze Zahl, die Antwort auf diese Frage ist. Die Menge der Zahlen musste um die der Brüche erweitert werden. Damit lautet die Antwort auf obige Frage x = 9/2 = 4.5. Ganze Zahlen und Brüche heißen zusammen rationale Zahlen.

Doch auch die rationalen Zahlen reichen nicht aus. So konnten Mathematiker zeigen, dass es keine rationale Antwort auf die Frage "Welche Zahl ergibt mit sich selbst multipliziert 2?" gibt. Für diese Aufgabe wurde die irrationale "Wurzel 2" erfunden. Rationale und irrationale Zahlen ergeben die reellen Zahlen.

Mit den reellen Zahlen kann man die Gleichung "x² = 2" lösen, "x² = -1" bleibt aber immer noch ohne Antwort, so lange man die Menge der Zahlen nicht noch ein weitere Mal erweitert und zwar um die imaginäre Zahl i = Wurzel -1. Dies tat der Mathematiker Leonhard Euler (1707-1783). Die Menge aller Zahlen, die aus reellen Zahlen und reellen Vielfachen von i zusammengesetzt sind, nennt man komplexe Zahlen.

Darstellung komplexer Zahlen

Die Standard-Schreibweise für eine komplexe Zahl ist die Summe aus zwei (reellen) Zahlen:

wobei i die Wurzel aus -1 darstellt. a heißt in diesem Fall Realteil von z, b nennt man den Imaginärteil von z.

Während die reellen Zahlen alle auf einer Zahlengeraden liegen, braucht man für die komplexen Zahlen eine Zahlenebene. Eine komplexe Zahl kann man sich in dieser Zahlenebene als Pfeil vorstellen, der über die Zahlen a und b bestimmt wird.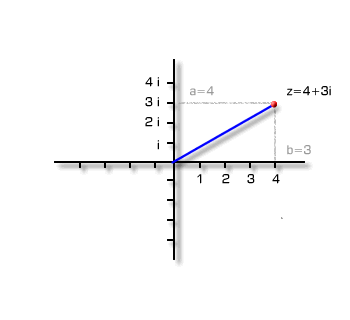

Eine komplexe Zahl lässt sich als Pfeil zeichnen.

Die Länge dieses Pfeils nennt man den Betrag |z| einer komplexen Zahl z. Es gilt:

Addition komplexer Zahlen

Zwei komplexe Zahlen werden addiert, indem ihre jeweiligen Real- und Imaginärteile addiert werden. Seien z₁ und z₂ zwei komplexe Zahlen:

Dann gilt für die Summe z₁ + z₂:

Dasselbe Ergebnis erhält man auch, wenn man die beiden Pfeile, die den komplexen Zahlen entsprechen, aneinanderlegt.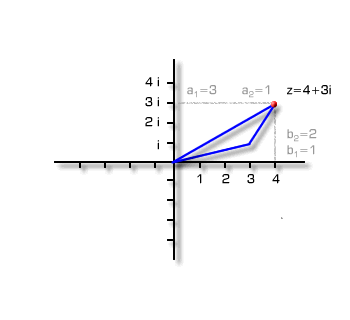

Zwei komplexe Zahlen werden addiert, indem man die Pfeile aneinanderlegt.