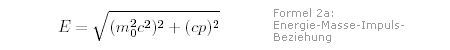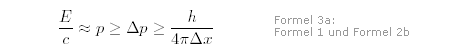Wozu beschleunigen?
Kleingedrucktes lesen

vorherige Seite | nächste Seite

Es ist eine der paradox klingenden Regeln der Natur: Je winziger die Strukturen, die man in der Natur ausmachen will, umso größer sind die dazu notwendigen Energien. Dies ist der Grund für die Größe von Teilchenbeschleunigern.

Fehlbenennung: Das Atom (gr. für unteilbar) stellte sich schon bald als teilbar heraus.

Gerne wird sie "Elementarteilchenphysik" genannt - jene Wissenschaft, die den Bauklötzen des Universums auf die Schliche kommen soll.

Ob die bisher gefundenen Puzzlesteine dabei wirklich elementar sind, kann heute niemand mit letzter Gewissheit sagen. Es sprechen zwar gute Gründe dafür, aber die Menschen "wussten" auch viele Jahre lang, dass das Atom unteilbar sei. Und gar nicht so lange davor, drehte sich die Sonne noch um die Erde - zumindest in den Köpfen der Menschen.

Und wie viel hat das bizarre Benehmen von Elektronen und Quarks eigentlich noch mit dem von Teilchen gemein? Der Quantentheorie zufolge wenig. Danach verhalten sich Quarks und Konsorten zwar wie Teilchen, wenn man sie erspäht, schaut man hingegen weg, so bewegen sie sich wie Wellen fort und werden mit Hilfe wabernder, den ganzen Raum durchziehender Quantenfelder beschrieben.

"Vielleicht-nicht-ganz-elementare-wabernde-Quantenfelder-Physik" ist aber auch keine Alternative zu "Elementarteilchenphysik". Das Los vieler Physiker fiel vielmehr auf "Hochenergiephysik". Damit beschreiben sie ihren Versuch, die Natur bei immer höheren Energien zu untersuchen und damit immer kleinere Strukturen zu beleuchten. Dieses Mehr an Energie ist der Grund, wieso Teilchenbeschleuniger im Laufe der Zeit immer größer geworden sind. Es ergibt sich aus einem eherne Naturgesetz: Je kleiner etwas ist, umso mehr Energie ist vonnöten, um es genau zu untersuchen. Kleingedrucktes zu lesen, strengt halt an.

Wieso so hohe Energien?

Eine mathematische Herleitung für das Gesetz vom Problem, Kleingedrucktes zu lesen, ergibt sich aus der Heisenbergschen Unschärfe-Relation und der Energie-Masse-Impuls-Beziehung der Relativitätstheorie. Nach der Heisenbergschen Unschärfe-Relation kann man Impuls und Ort eines Teilchens nicht beliebig genau messen. So sehr man sich auch bemüht, für beide Größen bleibt eine gewisse Unschärfe, deren Produkt mindestens von der Größenordnung der Planck-Konstante h ist. Der Impuls eines Teilchens hängt über die Energie-Masse-Impuls-Beziehung mit der Energie zusammen: 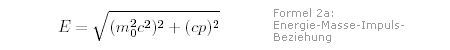Bei sehr schnellen Teilchen fällt der erste Term unter der Wurzel gegenüber dem zweiten nicht weiter ins Gewicht und kann getrost vernachlässigt werden. Es gilt dann: Wenn wir jetzt noch davon ausgehen, dass der Impuls eines Teilchens größer ist als die Unschärfe im Impuls, haben wir schon alles, was wir brauchen. Die Formeln 1 und 2b ergeben dann zusammen: 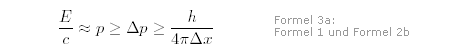Oder nach der Unschärfe im Ort aufgelöst: Die Ortsunschärfe kann also umso kleiner sein, je größer die Energie ist. Oder: Je kleiner die Dinge, die man sehen will, umso mehr Energie braucht man.

Trotz aller Einsicht: KworkQuark wird nicht in "Hochenergiephysik für alle!" umbenannt. Begriffe dienen der Verständigung und der Begriff "Teilchenphysik" macht seine Arbeit hervorragend.

vorherige Seite | nächste Seite