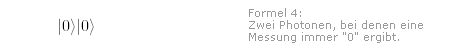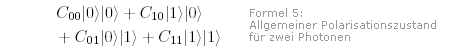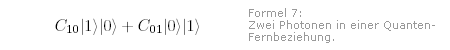Ein Photon Wenn wir die Polarisation eines Photons mit Hilfe eines Polarisators messen wollen, gibt es zwei Möglichkeiten: Entweder geht das Photon durch den Polarisator hindurch oder es wird reflektiert. Diese beiden Ergebnisse wollen wir mit "1" oder "0" beschreiben. Wenn die Messung immer das Ergebnis "0" liefert, so sei das Quant zuvor im Zustand  Falls das Ergebnis immer "1" lautet, soll der Zustand wie folgt bezeichnet werden:  Nach der Quantentheorie kann sich das Photon auch in einer Überlagerung aus diesen beiden Zuständen befinden. Im allgemeinen Fall wird dann mit einer Wahrscheinlichkeit von |c0|2 der Wert "0" gemessen und mit einer Wahrscheinlichkeit von |c1|2 lautet das Ergebnis "1". Für den Zustand des Quants schreibt man dann:  Zwei Photonen Sind nun zwei Quanten ins Spiel, verkompliziert sich die Sache nur gering. Der Quantentheorie zufolge muss man die Zustände der beiden Quanten nur auf eine ganz bestimmte Weise hintereinander schreiben. Dies ist eine Form der Multiplikation. 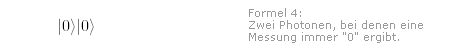 beschreibt einen Zustand, bei dem eine Messung bei beiden Photonen immer den Wert "0" ergeben würde. 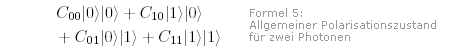 lautet der allgemeinste aller Quantenzustände bei zwei Photonen. Er bedeutet, dass bei einer Messung mit einer Wahrscheinlichkeit von |c00|2 bei beiden Quanten der Wert "0" gemessen wird, mit einer Wahrscheinlichkeit von |c01|2 bei ersten Quanten "0" und beim zweiten "1", mit einer Wahrscheinlichkeit von |c10|2 beim ersten Quant "1" und beim zweiten "0" und mit einer Wahrscheinlichkeit von |c11|2 bei beiden Quanten "1". An dieser Interpretation wird sichtbar, dass es bei der Quanten-Multiplikation auf die Reihenfolge der einzelnen Zustände ankommt. Es gilt:  Welche Werte im Allgemeinen c00, c01, c10 und c11 annehmen, ist vom Quantensystem abhängig. c00 und c11 könnten beispielsweise auch Null sein. Dann erhalten wir: 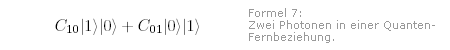 Was bedeutet das? Wenn wir die Polarisation des ersten Photons messen, werden wir mit einer Wahrscheinlichkeit von |c01|2 "0" erhalten und mit einer Wahrscheinlichkeit von |c10|2 "1". Bei dieser ersten Messung regiert der Zufall. Doch sobald wir das Ergebnis für das erste Quant kennen, wissen wir auch über das zweite Quant Bescheid. Denn der Quantenzustand legt fest, dass beide Quanten über entgegen gesetzte Einstellungen verfügen. Auch wenn die beiden Quanten Lichtjahre voneinander entfernt sind: Wenn wir in einer Messung die Eigenschaften des einen Teilchens festlegen, so gilt das auch für das andere Teilchen. |